One day in middle school, I was playing with perfect squares 0, 1, 4, 9, 16, 25, 36, 49, 64, 81…
Something neat pops out! A bunch of 9-ish things!
One number was 9
One number was 36, and 3+6=9
One number was 81, and 8+1=9
Adding the digits in each number together until we have all single digits (digital roots) like
81: 8+1=9
64: 6+4=10 and then 10: 1+0=1
We get a pattern:
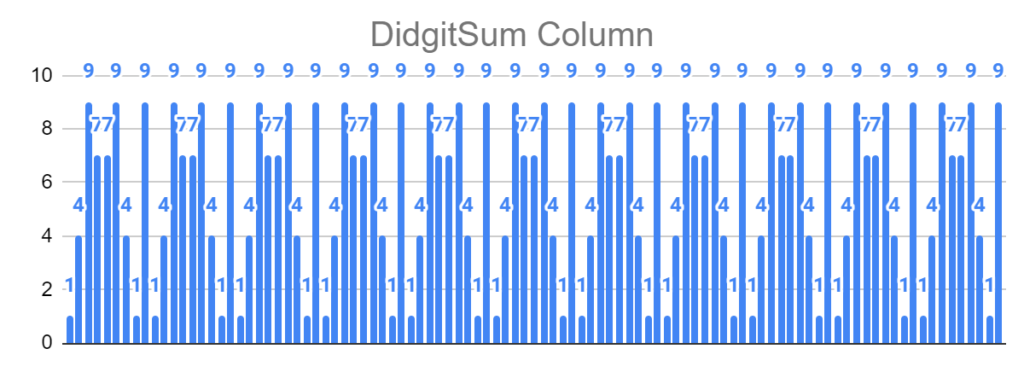
1 4 9 7 7 9 4 1 9 1 4 9 7 7 9 4 1 1 1 4 9 7 7 9 4 1 9
(1 4 9 7)-(7 9 4 1) 9 (1 4 9 7)-(7 9 4 1) 9 (1 4 9 7)-(7 9 4 1) 9
A beautiful periodicity!

You can actually catch part of this pattern in a common thing! When you replace the numbers in a typical multiplication table with their digital roots, this pattern makes up the diagonal. The Vedic Square is an abbreviated multiplication table (9×9) and so the first 8 elements of the pattern fall along its diagonal.
Also, how weird that 0 isn’t included, since 02=0?
I have to be missing part of the picture to not see why – do you know?
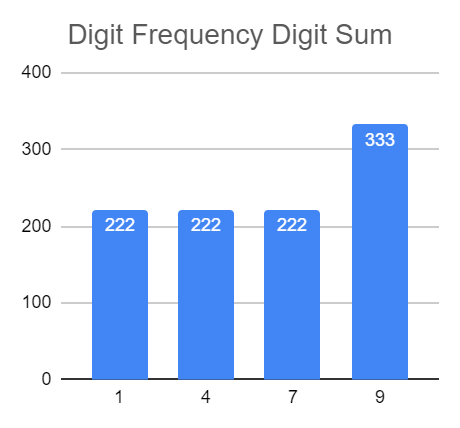
I haven’t played with more than the visual stuff yet, but I suspect we might find another neat thing based on how that looks if we take out further the series by individual summation steps, where if 822 = 6724, then
step 1: 6+7+2+4=19
step 2: 1+9=10
step 3: 1+0=1
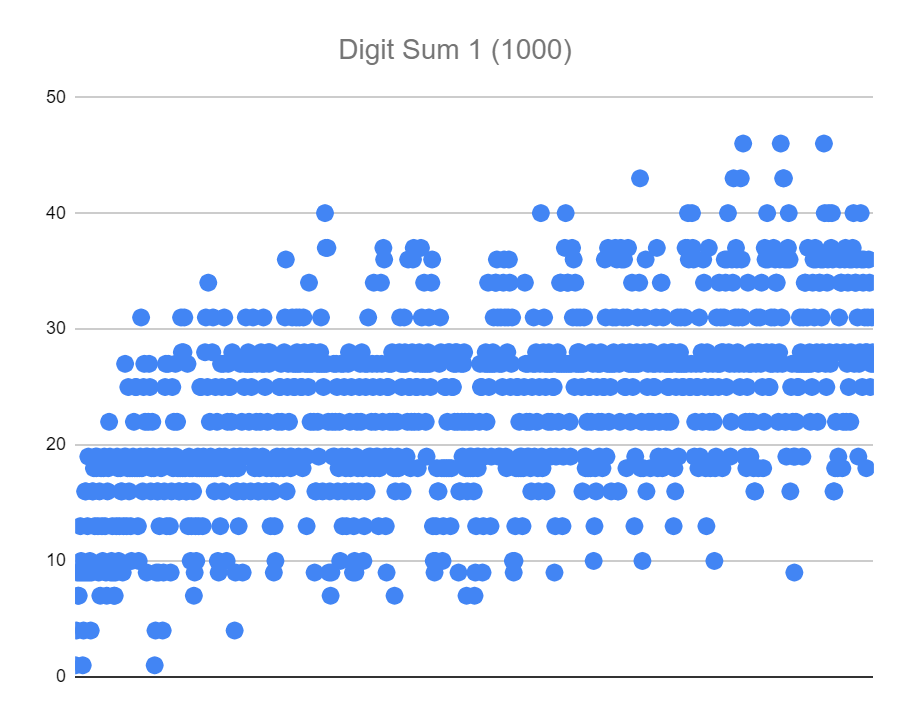
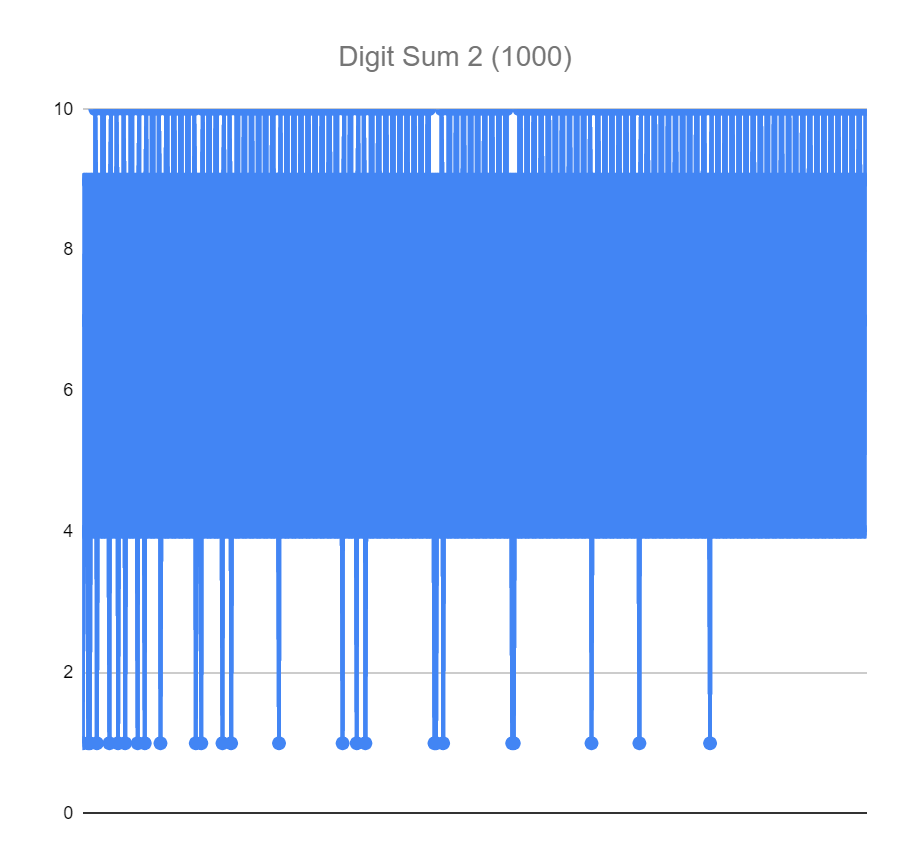
The workbook I played with this in is here 🙂
(see another beautiful periodicity in the Perfect Squares Last Digit Sequence)
1, 4, 9, 7, 7, 9, 4, 1, 9


Leave a Reply