The neat little patterns that sit in math are so beautiful and lovely. As a kid, I was playing with perfect squares and found these couple of patterns. They seemed like such big universal secrets to uncover for little me at the time! What beautiful patterns have you stumbled into?
Perfect Squares Last Digit Sequence
(more detailed explanation & graphs here)
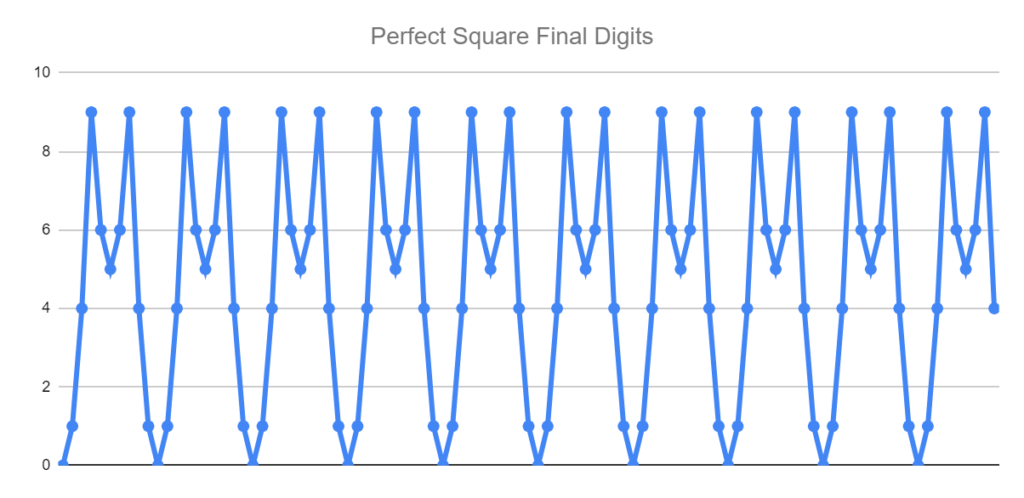
From the series of perfect squares 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 361…
The last digits of each term make up a repeating bit, 0 (1496) 5 (6941), so stringing them together makes this really pretty periodicity!
0 (1496) 5 (6941) 0 (1496) 5 (6941) 0 (1496) 5 (6941) 0 (1496) 5 (6941) 0 (1496) 5 (6941) 0
Perfect Squares Digital Root Sequence
(slightly more detailed explanation & graphs here)
Still playing with perfect squares 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 361…
Adding the digits in each number together (for 81: 8+1=9) until we have all single digits, we get the repeating pattern (1 4 9 7)-(7 9 4 1) 9, strung together, you get another beautiful periodicity!
(1 4 9 7)-(7 9 4 1) 9 (1 4 9 7)-(7 9 4 1) 9 (1 4 9 7)-(7 9 4 1) 9 (1 4 9 7)-(7 9 4 1) 9

You can actually catch part of this pattern in a common thing! When you replace the numbers in a typical multiplication table with their digital roots, this pattern makes up the diagonal. The Vedic Square is an abbreviated multiplication table (9×9) and so the first 8 elements of the pattern fall along its diagonal.
Also, how weird that 0 isn’t included, since 02=0?
I have to be missing part of the picture to not see why – do you know?
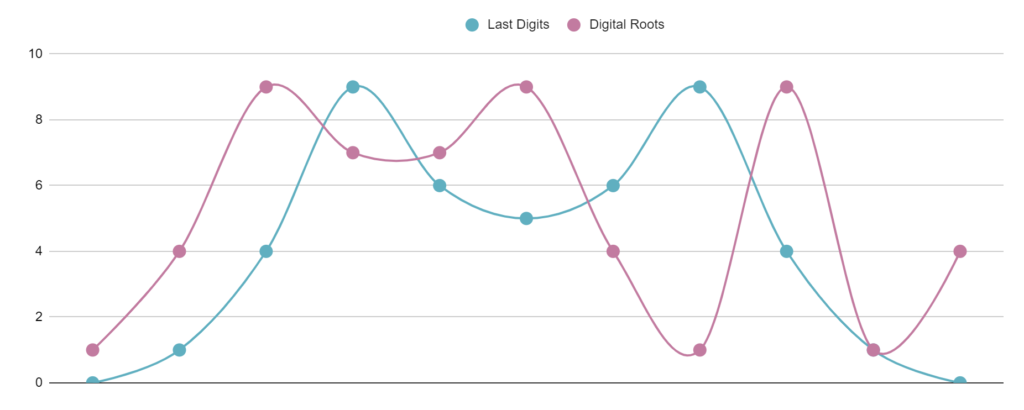
Just for fun, here are both together!
The workbook I played with this in is here 🙂

0 Comments